Chapter 2 Stacks and Queues
Two of the more common data objects found in computer algorithms are stacks and queues. Both of these objects are special cases of the more general data object, an ordered list.
A stack is an ordered list in which all insertions and deletions are made at one end, called the top. A queue is an ordered list in which all insertions take place at one end, the rear, while all deletions take place at the other end, the front. Given a stack S=(a[1],a[2],.......a[n]) then we say that a1 is the bottommost element and element a[i]) is on top of element a[i-1], 1<i<=n. When viewed as a queue with a[n] as the rear element one says that a[i+1] is behind a[i], 1<i<=n.
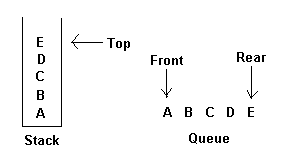
The restrictions on a stack imply that if the elements A,B,C,D,E are added to the stack, n that order, then th efirst element to be removed/deleted must be E. Equivalently we say that the last element to be inserted into the stack will be the first to be removed. For this reason stacks are sometimes referred to as Last In First Out (LIFO) lists. The restrictions on queue imply that the first element which is inserted into the queue will be the first one to be removed. Thus A is the first letter to be removed, and queues are known as First In First Out (FIFO) lists. Note that the data object queue as defined here need not necessarily correspond to the mathemathical concept of queue in which the insert/delete rules may be different.
You can see the algorithms you want by clicking on the items below:
- Adding an element into a stack.
- Deleting an element from a stack.
- Adding an element into a queue.
- Deleting an element from a queue.
One natural example of stacks which arises in computer programming is the processing of procedure calls and their terminations. Suppose we have four procedures as below:
The MAIN procedure invokes procedure A1. On completion of A1 exection of MAIN will resume at location r. The adress r is passed to A1 which saves it in some location for later processing. A1 then invokes A2 which in turn invokes A3. In each case the invoking procedure passes the return address to the invoked procedure. If we examine the memory while A3 is computing there will be an implicit stack which looks like
(q,r,s,t)
The first entry, q, is the address to which MAIN returns control. This list operates as a stack since the returns will be made in the reverse order of the invocations. Thus t is removed before s, s before r and r before q. Equivalently this means that A3 must finish processing before A2, A2 before A1, and A1 before MAIN. This list of return addresses need not be maintained in consecutive locations. For each procedure there is usually a single location associated with the machine code which is used to retain the return address. This can be severely limiting in the case of recursive and re-entrant procedures, since every time we invoke a procedure the new return address wipes out the old one. For example, if we inserted a call to A1 within procedure A3 expecting the return to be at location u, then at execution time the stack would become (q, u, s, t) and the return address r would be lost. When recursion is alloed, it is ni longer adequate to reserve one location for the return address of each procedure. Since returns are made in the reverse order of calls, an elegant and natural solution to this procedure return problem is afforded through the explicit use of a stack of return addresses. Whenever a return is made, it is to the top address in the stack.
An interactive example will make the subject of stacks and queues clearer.